Um modelo simples para a taxa de câmbio
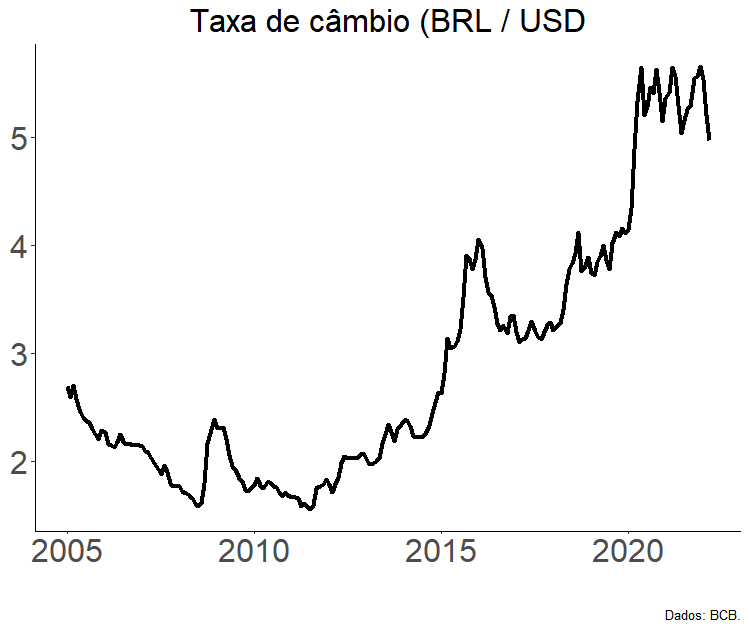
Apresento aqui um exercício macroeconométrico para explicar o comportamento da taxa de câmbio BRL/USD.
Para onde vai a taxa de câmbio? A resposta para essa pergunta vale muito, muito dinheiro. E traz consigo dor de cabeça (além de humildade) aos economistas que se propõem a traçar cenários (macro)econômicos. Desde pelo menos Meese e Rogoff sabemos que é difícil relacionar teoria e projeções macroeconômicas .1 Mas a Barbara Rossi nos lembra que a literatura avançou muito nesse sentido.2
O que eu proponho aqui está menos para um modelo que projete a taxa de câmbio nominal (sinto desapontar a leitora esperançosa) e mais para um modelo que ajude a explicar o seu comportamento. Deixo à disposição daqueles interessados o código em R que utilizei para fazer o exercício e fico no aguardo para que retornem tanto com especificações alternativas, como com a identificação de quaisquer erros e imprecisões. Vamos aos dados.
Variáveis do modelo
Genericamente, é um modelo que resulta da amalgama da teoria da paridade descoberta de taxa de juros e da determinação pelos fluxos comerciais taxa de câmbio (nominal, neste caso). Utilizo valores médios mensais e uma amostra que vai de janeiro de 2005 a março de 2022.
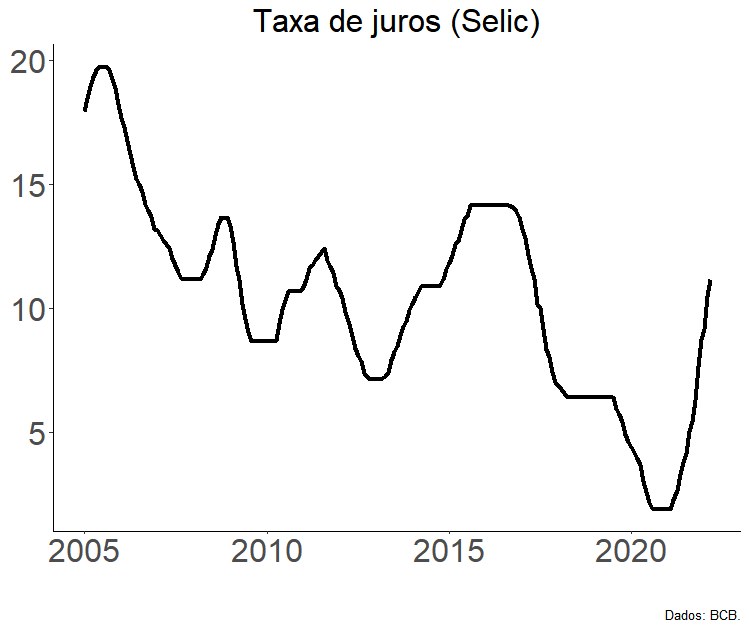
Diferencial de juros
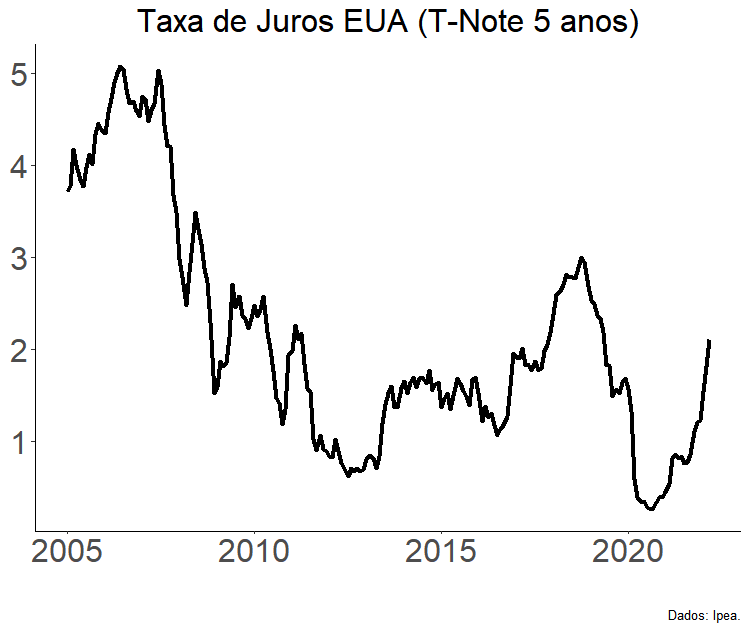
Pela teoria da paridade descoberta da taxa de juros, os diferenciais de juros domésticos e internacionais direcionariam os fluxos financeiros de curto prazo e, com eles, o comportamento da taxa de câmbio nominal. Utilizei no modelo a diferença entre a taxa Selic anualizada e os juros dos T-Notes de cinco anos dos EUA.
Embora as taxas de juros incorporem prêmios de risco associados à dinãmica de títulos públicos, sabemos que existe um prêmio pelo risco cambial que pode tornar os modelos viesados, especialmente em economias desenvolvidas.3 Como não observamos esse prêmio de risco diretamente, considerei duas variáveis que serviriam para ajudar a capturar a sua dinâmica: EMBI+ e um índice de incerteza da política econômica.
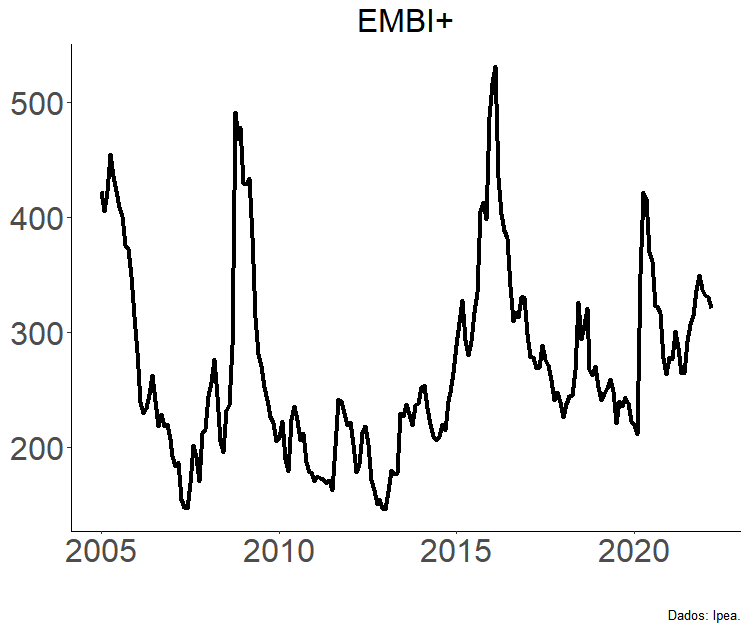
Risco: EMBI+
O EMBI+ é uma medida de risco em títulos de dívida soberana super conhecido, ainda que há quem argumente que o CDS, por exemplo, seja uma medida superior.
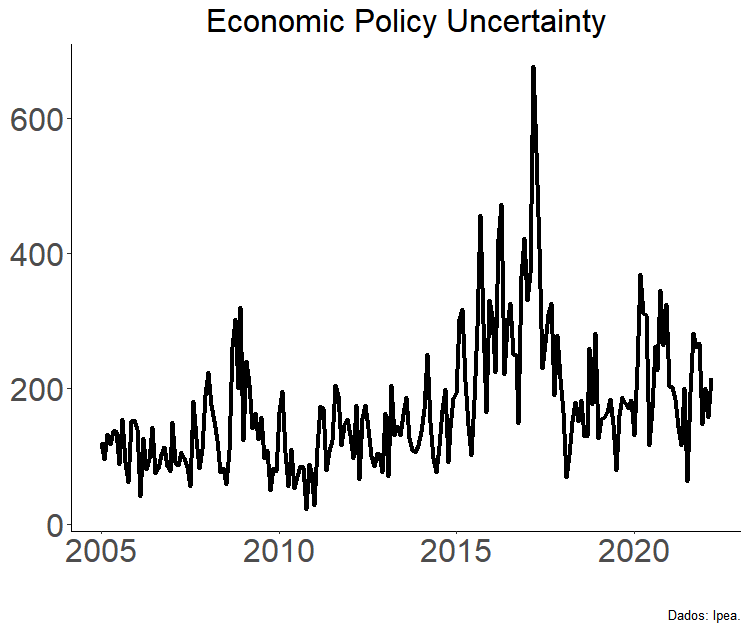
Incerteza: Economic Policy Uncertainty
Do ponto de vista das incertezas acerca da condução da política econômica, o Economic Policy Uncertainty index pode ser uma medida interessante para complementar o que o EMBI+ não conseguir capturar.
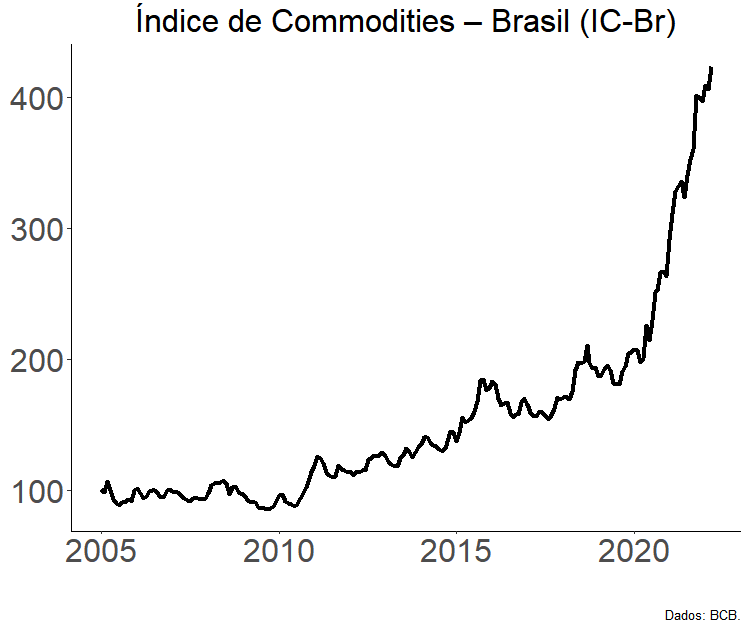
Bloco “comercial”
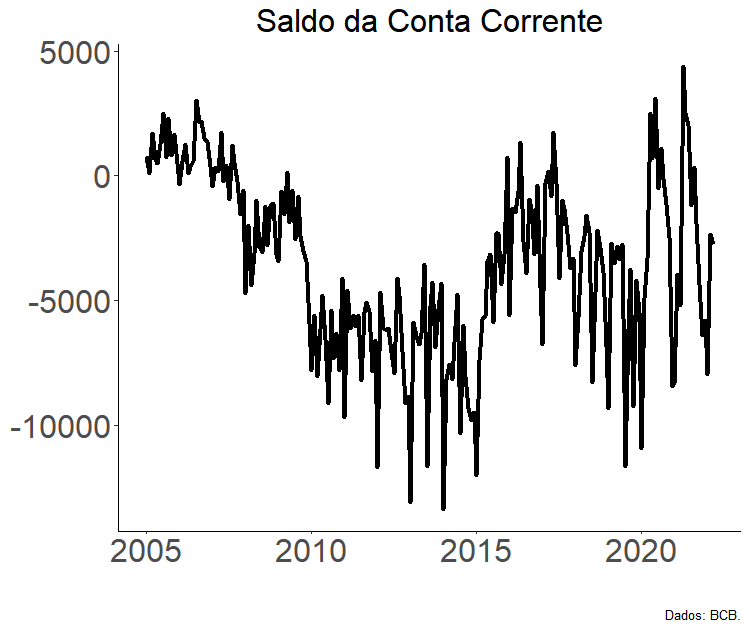
Ao bloco “financeiro”, vamos adicionar a dinâmica mais comercial, aqui representada por duas variáveis: o índice de commodities do Banco Central do Brasil e o saldo da conta corrente.
Resultado
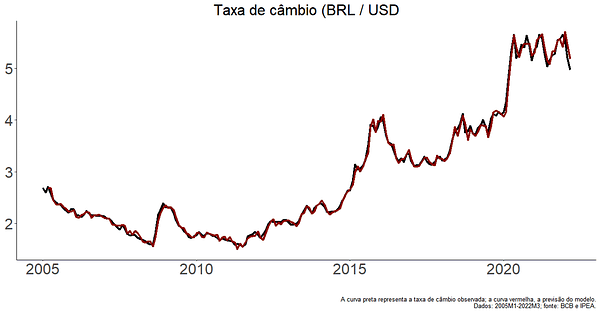
Antes de apresentar o resultado, vale expor que i) utilizei as variáveis em primeira diferença (em alguns casos, utilizei a diferença logarítmica para aproximar taxas de variação), ii) a regressão múltipla foi feita com base em estimadores bayesianos, cuja motivação é a pequena amostra, iii) adicionei dummies para a crise de 2008, a depressão de 2014-2016 e a crise da Covid-19 e iv) claramente o primeiro problema deste modelo é a endogeneidade entre algumas variáveis, portanto, este exercício possui limitações e vieses relacionados à esse aspecto. De toda forma, acho que vale a “brincadeira” e parece que ajuda a explicar alguma coisa dos movimentos mensais da taxa de câmbio nominal:
E você, o que acrescentaria ao modelo? Manda sugestões, códigos, etc, para compartilharmos na newsletter!
Código em R para replicar o exercício
#### Packages ####
library(ipeadatar)
library(rbcb)
library(xts)
library(ggplot2)
#search <- search_series(terms = "taxa de câmbio", fields = c('name'), language = "br")
#### Data ####
#### EMBI+ ####
embi <- ipeadata("JPM366_EMBI366", language = "br", quiet = FALSE )
embi <- data.frame( time = embi$date,
embi = embi$value )
embi$time <- as.Date( embi$time, format='%d/%m/%Y')
embi$embi <- xts( embi$embi, order.by = embi$time )
embi <- apply.monthly( embi$embi, FUN=mean )
embi <- ts( embi, start = c( 1994, 4 ), freq = 12 )
embi <- window( embi, start = c( 2005, 1 ), end = c( 2022, 3 ), frequency = 12 )
#### Current Account ####
ca <- ipeadata("PAN12_STC12", language = "br", quiet = FALSE) # Transações correntes - saldo (BPM6)
ca <- data.frame( time = ca$date,
ca = ca$value )
ca$time <- as.Date( ca$time, format='%d/%m/%Y')
ca$ca <- xts( ca$ca, order.by = ca$time )
ca <- apply.monthly( ca$ca, FUN=mean )
ca <- ts( ca, start = c( 1995, 1 ), freq = 12 )
ca <- window( ca, start = c( 2005, 1 ), end = c( 2022, 3 ), frequency = 12)
#### TNote ####
tnote <- ipeadata("VALOR12_TNOTES512", language = "br", quiet = FALSE) #taxa de juros - T-Note (5 anos)
tnote <- data.frame( time = tnote$date,
tnote = tnote$value )
tnote$time <- as.Date( tnote$time, format='%d/%m/%Y')
tnote$tnote <- xts( tnote$tnote, order.by = tnote$time )
tnote <- apply.monthly( tnote$tnote, FUN=mean )
tnote <- ts( tnote, start = c( 1953, 4 ), freq = 12 )
tnote <- window( tnote, start = c( 2005, 1 ), end = c( 2022, 3 ), frequency = 12)
#### Selic ####
selic <- get_series(4189, start_date = '2005-01-03' )
selic <- data.frame(time=selic$date, selic=selic$`4189`)
selic$time <- as.Date(selic$time, format='%d/%m/%Y')
selic$selic <- xts(selic$selic, order.by = selic$time)
selic <- apply.monthly(selic$selic, FUN=mean)
selic <- ts(selic, start=c( 2005,1 ), freq=12 )
selic <- window( selic, start = c( 2005, 1 ), end = c( 2022, 3 ), frequency = 12 )
#### IC ####
ic <- get_series(27574, start_date = '1998-01-31' ) # Índice de Commodities - Brasil
ic <- data.frame( time = ic$date,
ic = ic$`27574` )
ic$time <- as.Date( ic$time, format='%d/%m/%Y')
ic$ic <- xts( ic$ic, order.by = ic$time )
ic <- apply.monthly( ic$ic, FUN=mean )
ic <- ts( ic, start = c( 1998, 1 ), freq = 12 )
ic <- window( ic, start = c( 2005, 1 ), end = c( 2022, 3 ), frequency = 12 )
#### Economic Policy Uncertainty ####
url <- 'https://www.policyuncertainty.com/media/Brazil_Policy_Uncertainty_Data.xlsx'
download.file(
url = url,
destfile = "epu.xlsx",
mode = "wb"
)
epu <- readxl::read_excel(
path = "epu.xlsx",
sheet = 'Brazil EPU Index',
range = "C2:C380",
col_names = FALSE
)
epu <- ts( epu$...1, start = c( 1991, 1), freq = 12 )
epu <- window(epu, start = c(2005, 1), end = c( 2022,3 ), frequency = 12 )
#### Taxa de Câmbio ####
e <- get_series(1, start_date = '2005-01-03' ) #
e <- data.frame( time = e$date,
e = e$`1` )
e$time <- as.Date( e$time, format='%d/%m/%Y')
e$e <- xts( e$e, order.by = e$time )
e <- apply.monthly( e$e, FUN=mean )
e <- ts( e, start = c( 2005, 1 ), freq = 12 )
e <- window( e, start = c( 2005, 1 ), end = c( 2022, 3 ), frequency = 12 )
#### Data treatment
dlne = diff( log( e ) )
dlne1 = dlne %>% lag.xts(k = 1)
dspread = diff( selic - tnote )
dlnembi = diff( log( embi ) )
dlnic = diff( log( ic ) )
dlnepu = diff( log( epu ) )
dca = diff( ca )
d2014 = ts( ifelse( time( dlne ) > 2014.00 & time( dlne ) < 2017.99, 1, 0 ),
start = c( 2005, 2 ), frequency = 12 ) # Dummy for the 2014-2016 recession
dcovid = ts( ifelse( time( dlne ) > 2020.00 & time( dlne ) < 2022.00, 1, 0 ),
start = c( 2005, 2 ), frequency = 12 ) # Dummy for the covid recession
d2008 = ts( ifelse( time( dlne ) > 2008.25 & time( dlne ) < 2010.25, 1, 0 ),
start = c( 2005, 2), frequency = 12 ) # Dummy for the 2014-2016 recession
#### Model ####
library(MCMCpack)
dados <- data.frame( dlne, dlne1, dspread, dlnembi, dlnic, dca, dlnepu,
d2014, dcovid, d2008)
colnames(dados) <- c("Dlne", "Dlne(-1)", "Dspread",
"DlnEMBI+", "DlnIC-Br", "CA", "EPU",
"d2014", "dcovid", "d2008")
e_mcmc <- MCMCregress( dlne ~ dlne1 + dspread + dlnembi + dlnic + dca + dlnepu +
d2014 + dcovid + d2008, data = dados,
seed = 1301, burnin = 1000, verbose = 0)
#verbose <> 0 mostra o processo de iterações.
summary(e_mcmc)
beta0 = median( e_mcmc[,1] ); #intercept
beta1 = median( e_mcmc[,2] ); #dlne1
beta2 = median( e_mcmc[,3] ); #dspread
beta3 = median( e_mcmc[,4] ); #dlnembi
beta4 = median( e_mcmc[,5] ); #dlnic
beta5 = median( e_mcmc[,6] ); #dca
beta6 = median( e_mcmc[,7] ); #dlnepu
delta1 = median( e_mcmc[,8] ); #d2014
delta2 = median( e_mcmc[,9] ); #dcovid
delta3 = median( e_mcmc[,10] ); #d2008
#### Forecast ####
dlnef = ts( beta0 + beta1 * dlne1 + beta2 * dspread + beta3 * dlnembi +
beta4 * dlnic + beta5 * dca + beta6 * dlnepu +
delta1 * d2014 + delta2 * dcovid + delta3 * d2008,
start = c( 2005, 3 ), frequency = 12 )
forecast = matrix( data = NA, nrow = length(dlnef)+1, ncol = 1)
forecast[1] = e[1]
for ( t in 2:length(e) ) {
forecast[ t ] = e[ t-1 ] * ( 1 + dlnef[ t-1 ] )
}
forecast = ts( forecast, start = c( 2005, 1), frequency = 12)
data = data.frame( e, forecast, dates=time(e) )
colnames(data) <- c( "e", "Forecast", "dates")
#data = subset( data, dates > 2007 )
ggplot(data) + geom_line(aes(x = dates, y = e ), size = 1.5, colour = "black") +
geom_line(aes(x = dates, y = Forecast ), size = 1.5, colour = "darkred") +
theme_classic() +
# geom_rect(data=recessions, aes(xmin=Peak,
# xmax=Trough, ymin=-Inf, ymax=+Inf), fill='gray', alpha=0.2) +
labs(x = "", y = "") + # ylab( TeX( "$y_t$" ) ) + theme(aspect.ratio=1) +
ggtitle( "Taxa de câmbio (BRL / USD" ) +
theme(plot.title = element_text( size = 24, hjust = 0.5) ) +
theme(axis.text = element_text(size = 24) ) +
theme(axis.title.y = element_text(size = 24, angle = 360, vjust = 0.5, hjust=1)) +
theme(axis.title.x = element_text(size = 24, vjust = 0.5, hjust=1)) +
theme(text = element_text(size= 12) ) +
labs( caption = "A curva preta representa a taxa de câmbio observada; a curva vermelha, a previsão do modelo.
Dados: 2005M1-2022M3; fonte: BCB e IPEA.")Meese, R. A., & Rogoff, K. (1983). Empirical exchange rate models of the seventies: Do they fit out of sample?. Journal of international economics, 14(1-2), 3-24.
Rossi, B. (2013). Exchange rate predictability. Journal of Economic Literature, 51(4), 1063-1119.
Fama, E. F. (1984). Forward and spot exchange rates. Journal of Monetary Economics, 14(3), 319-338.