Um exercício de projeção para a produção industrial de janeiro de 2025
Projeção para a Pesquisa Industrial Mensal: Produção Física - Brasil.
Hoje começa a nova turma do meu curso de Projeções Macroeconômicas: Teoria e Prática. Na primeira aula, vou abordar o conceito de funções de perda e critérios simétricos e assimétricos na avaliação das projeções. Como é frequente nos meus cursos, além de aprofundar os conceitos teóricos, teremos uma aplicação prática. Vamos trabalhar com os dados da produção industrial e avaliar o comportamento projetado para 2025.
Neste breve texto, vou compartilhar os resultados desse exercício de projeção.
Modelos
Fiz um exercício análogo ao de Fotios Petropoulos e Ivan Svetunkov no artigo A simple combination of univariate models, publicado no International Journal of Forecasting: utilizei alguns modelos univariados (Holt-Winters aditivo, Holt-Winters multiplicativo, “auto” Holt-Winters, “auto” ARIMA e Complex Exponential Smoothing) e duas combinações simples: a média e a mediana das projeções.1
Considerei dois tipos de amostra para o treinamento dos modelos: em expansão e de tamanho constante.
Amostra em expansão
Na amostra de treinamento em expansão, comecei com 75% dos dados (que se iniciam em janeiro de 2002, sem ajuste sazonal) e, a cada iteração, adicionei uma observação. Considerei o menor horizonte possível para uma projeção: um período à frente (sem a necessidade, portanto, da construção de cenários por meio das projeções recursivas).
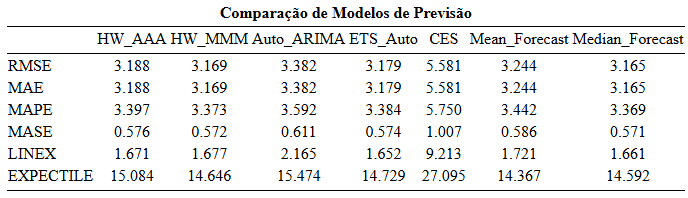
Para avaliar as projeções, eu utilizei quatro métricas simétricas (RMSE, MAE, MAPE e MASE) e duas assimétricas (Linex e do tipo Expectile). Os resultados foram interessantes e estão sintetizados na Tabela 1. (Importante: os decimais na tabela são separados por ‘ponto’ e não por ‘vírgula’).
Em média, o modelo com a melhor performance com base no RMSE, no MAE (dado o horizonte de previsão igual a um período, o RMSE será igual ao MAE), no MAPE, no MASE e no Linex é aquele que resulta da combinação simples por meio da mediana dos modelos, exatamente como prescrevem Petropoulos e Svetunkov (veja o apêndice ao final do texto com as equações para cada uma das métricas). Apenas no critério do tipo Expectile a utilização da média (ao invés da mediana) seria mais recomendada.
Amostra de tamanho constante
Uma alternativa à janela em expansão é avaliar o comportamento dos modelos quando o tamanho da amostra de treinamento é constante, mas móvel. Defini que a amostra deveria ter 36 observações e avaliei o comportamento dos modelos com as mesmas métricas que anteriormente, cujos resultados são apresentados na Tabela 2.
Nesse caso, embora a combinação dos modelos por meio da mediana tenha uma boa performance, o auto ETS se destaca com base no RMSE, MAR, MAPE, MASE e no critério do tipo Expectile, ao passo que o Holt-Winters multiplicativo é o melhor modelo com base no critério Linex. Obviamente, outros tamanhos de janela podem gerar outras conclusões (e uma área de estudo interessante é a de descobrir o tamanho ótimo dessa janela).
Projeções
Findas as análises, no exercício de projeções eu seguirei com a mediana dos modelos. Estimei o modelo nas últimas 36 observações disponíveis e fiz uma projeção para os doze meses de 2025, ainda que o exercício de avaliação tenha sido realizado apenas com o horizonte de um período (o mais indicado, na minha opinião, seria escolher doze modelos diferentes: o melhor para cada tipo de horizonte). O gráfico a seguir apresenta a projeção para os dados sem ajuste sazonal.
É possível verificar que não há projeção de um ano muito exuberante para a indústria no Brasil, ainda que em nível maior do que o que operou em 2024 (ao ajustar sazonalmente os dados, prevê-se que o índice médio da indústria em 2025 seja 0,8% maior do que em 2024, em linha com a minha projeção de crescimento de 0,9% para a indústria com base nas contas nacionais).
Por fim, o modelo, projeta um crescimento de 2,15% frente ao mesmo mês do ano anterior e de 0,16% frente a dezembro (nos dados com ajuste sazonal).
Apêndice: Métricas
Métricas simétricas
Métricas Assimétricas
Para quem tiver interesse nos modelos ARIMA, recomendo o meu material do curso de Econometria de Séries Temporais.